Análise Estatística de Dados

Teoria de Amostragem e Cálculo Amostral

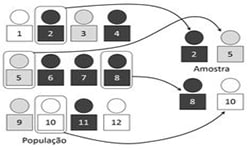
 A Teoria da Amostragem diz respeito à estratégia a ser utilizada para seleção de uma amostra, além de fornecer mais informações acerca do modo de ação no que toca ao uso de uma metodologia de amostragem para uma investigação ou estudo.

Dessa forma, assim que o pesquisador estabeleça a população potencial para sua investigação, ele deve fixar critérios de escolha dos seus constituintes, que podem ser para incluir ou excluir pessoas que integrarão o estudo, sendo que uma amostra é considerada representativa caso as suas características se pareçam o mais possível às da população-alvo.

É assim importante que a amostra ilustre não apenas as variáveis sob investigação, mas também outros fatores que possam exercer algum impacto sobre as variáveis da pesquisa, como a idade, o sexo, a escolaridade e o rendimento.

Assim, o potencial de representatividade de uma amostra, é avaliado através da comparação entre as médias da amostra com as da população-alvo, sendo o conceito de amostra definido como o conjunto de elementos extraídos de uma população, que de modo suficiente, representem essa população. Assim sendo, após a definição da amostra, estaremos prontos para efetuar a análise dos resultados como se investigássemos a população na sua totalidade.

A amostra será sempre finita, entretanto, quanto maior for esta, mais valiosa é a pesquisa. No entanto, como sempre há dúvidas de que todas as características da população estão representadas numa amostra, já que estas não costumam ser conhecidas, partindo-se do princípio de que um certo grau de erro sempre estará presente.  

Assim, os resultados de investigações por amostragem estão sempre expostos a uma determinado grau de incerteza, não apenas porque se estudou somente uma parte da população, mas também devido a falhas de mensuração, sendo que tal grau de incerteza pode ser diminuído com o crescimento do tamanho da amostra e através do uso de ferramentas mais eficazes de mensuração.

A teoria da amostragem tem em conta duas dimensões:

1ª) Dimensionamento da Amostra e

2ª) Composição da Amostra, sendo inúmeros os meios de determinação da extensão de uma amostra. No entanto, será preciso voltar a atenção para os seguintes pontos:

1. Análise do inquérito ou roteiro da entrevista e selecionar uma ou mais variáveis que avalie serem mais significativas para o estudo.
2. Conferir o nível de mensuração da variável: nominal, ordinal ou intervalar;
3. Ter em conta a extensão da população: infinita ou finita
4. O tamanho da amostra é determinado em função do grau de mensuração da variável selecionada.
5. São inúmeras as fórmulas que possibilitam o cálculo da extensão de uma amostra e sua seleção dependerá do que é estudado ou dos parâmetros à disposição.

A seguir são apresentadas algumas fórmulas para cálculos amostrais:

Variável intervalar e população finita

Quando a variável é de nível intervalar e a população é considerada finita, determina-se o tamanho da amostra pela fórmula:

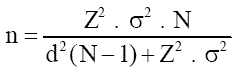
onde:

Z = abscissa da normal padrão

N = tamanho da população

d = erro amostral

Variável qualitativa (nominal ou ordinal) e população finita

Quando a variável for nominal ou ordinal e a população for considerada finita, determina-se a extensão da amostra através da fórmula:

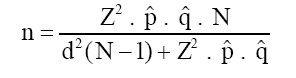
onde:

Z = abscissa da normal padrão

N = tamanho da população

p = estimativa da proporção.

𝑞 = 1- p

d = erro amostral

Assim, as fórmulas citadas acima são básicas para toda modalidade de composição da amostra. No entanto, existem fórmulas específicas de acordo com o critério relativo à composição da amostra. Caso não existam condições de previsão do possível valor para 𝑝, será admitida 𝑝 =0,50 pois, assim, teremos a maior extensão da amostra, considerando constantes os outros elementos.

Determinação da Margem de Erro da Amostra

A Margem de erro de uma amostra que representará de modo aproximado uma população é explicada da seguinte forma: Pot exemplo caso uma investigação possua uma margem de erro de 3% e um certa doença teve 20% de prevalência na amostra formada, podemos falar que, naquele momento, na população em questão, ela terá uma prevalência entre 17% e 23% (20% menos 3% e 20% mais 3%). O nível de confiança é definido como um parâmetro utilizado pelas investigações, que é frequentemente de 95%, que significam que caso realizemos uma nova pesquisa, com uma amostra de igual extensão, nas mesmas datas e lugares e com a mesma ferramenta para coleta de dados, existirá uma probabilidade de 95% de que os resultados sejam iguais e uma probabilidade de 5% de que tudo seja diferente.

Fórmula para conhecer a margem de erro padrão

sp =raiz quadrada de (p. q) /n

De acordo com Agranonik e Hirokata (2009), é notório que a extensão da amostra para estimar uma proporção cresce, quando o nível de confiança do intervalo aumenta ou quando é reduzida a margem de erro. Por isso, caso o objetivo seja fazer a comparação entre proporções, a extensão da amostra aumentará, quando for diminuído o nível de significância, quando é aumentada a eficácia do teste, ou quando for reduzida a menor diferença relevante que almeja-se identificar entre as proporções.

Assim sendo, caso seja identificado um efeito de significância, igual ou superior ao estabelecido no cálculo, ele será percebido como importante do ponto de vista estatístico. Já ao ser estimada uma proporção por meio de intervalo de confiança, para reduzirmos a extensão da amostra, será preciso reduzir o nível de confiança, ou fazer crescer a margem de erro, sendo que a prevalência aplicada deve ser a encontrada em pesquisas anteriores conduzidas em uma amostra advinda de uma população parecida e de forma aproximada ao da investigação atual.

Entretanto, é facto conhecido que, em algumas situações, há limitações à extensão da amostra, por causa de recursos financeiros ou do tempo de recolha. No entanto, o tamanho da amostra deve ser o reflexo do verdadeiro objetivo da investigação, no sentido da extensão de efeito ou precisão do cálculo da estimativa

Exemplo de cálculo de tamanho de amostra para uma proporção

Almeja-se estimar a prevalência do tabagismo em jovens do Porto, com nível de confiança de 95% e margem de erro de 0,05. Não havendo estudos prévios, é possível utilizar a proporção de 50% na fórmula 2, sendo obtido o seguinte tamanho de amostra:

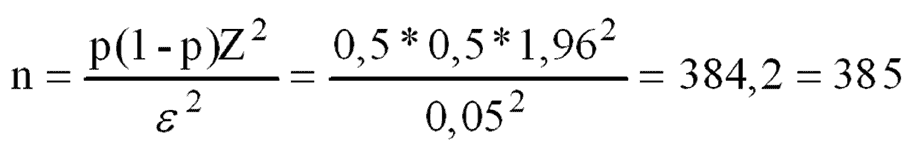
p = 0,50

1- p = 1- 0,50 = 0,50

Nível de confiança: 95% Z = 1,96 

É relevante notar que o cálculo da extensão da amostra ilustra o número mínimo necessário de indivíduos que devem ser entrevistados para alcançar um determinado objetivo. Assim, caso o valor auferido não seja um número inteiro, ele deverá ser arredondado para mais.

Para determinação da extensão da amostra a fim de comparar 2 proporções, é essencial que o investigador defina:

1- Qual a hipótese nula e decida se a hipótese alternativa é uni ou bidirecional;

2- A estimativa da magnitude de efeito e a variabilidade em termos de p1 (proporção de sujeitos em um dos grupos) e p2 (proporção de sujeitos com o desfecho no outro grupo);

3- O nível de significância (α) e o poder (1 – β).

A extensão da amostra para comparar 2 proporções (p1 e p2), para grupos de igual tamanho, pode ser estimada pelo uso da fórmula que segue onde:

n: é o número de sujeitos necessários em cada um dos grupos

p1: é a proporção esperada para o grupo 1,

p2: é a proporção esperada para o grupo 2

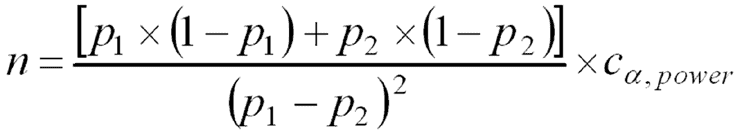
Bibliografia

Agranonik, M e Hirokata, V. Cálculo de tamanho de amostra: proporções. Revista HCPA. 2011; 31 (3): 382-388. Seção de Bioestatística.

Pocinho, M. (2009) Teoria e exercícios passo-a-passo: Amostra e tipos de amostragem. Publicado por Research Gate. https://www.researchgate.net/publication/268150358